Special Relativistic Contraction and Mass Increase
Derived From Physical Models
Introduction
It is well known that the scientists who developed Relativity, quantum mechanics and particle physics had mathematical abilities that are beyond most of us. It is also well known that they used those abilities to produce mathematical models of the aforementioned subjects.
Before about 1900, scientists also produced mathematical models to describe and predict physical phenomena, but they preferred to base their mathematical models on physical models. The kinetic theory of gases, for example, involves complex-looking mathematical equations, but was based on the physical model that particles in a gas bounce off of one another and bounce off the walls of the vessel containing the gas.
Since 1900, however, the seemingly non-intuitive aspects of the "newer" physics have led physicists to all but abandon the use of physical models. This has kept ordinary people, who know only elementary algebra, geometry, and maybe a little calculus, from ever trying to get a handle on such difficult subjects. But here, everyone makes the same assumptions
Actually, one of the developers of particle physics, Murray Gell-Mann, used the esoteric mathematics of Group Theory to develop a particle mathematical model he called "The Eightfold Way". But later, he realized that it corresponded to a physical model in which protons and particles that decay leaving protons are each composed or 3 particles he called quarks, while other particles, known as mesons, are each composed of a quark and an anti-quark.
So, could it be that other mathematical models are related to corresponding physical and intuitive models? To test this, one needs to see what equations intuitive physical models lead to. If they lead to the very same equations produced originally, through esoteric mathematics, is there any reason not to use physical models as an aid to understanding for those of us not well-versed in math? In this paper, we will explore the use of physical models and simple algebra and geometry to derive the equations for Special Relativistic Contraction, and for Special Relativistic Mass Increase.
Special Relativistic Contraction Derived From a Physical Model
The first special relativistic effect that was predicted was that if an object moves rapidly past you, it will appear shorter than when it is not moving. This was predicted mathematically by Lorentz in 1890, and by Einstein in 1905.
This same apparent shortening can be shown using a physical model. In the model, a stationary person attempts to hit a stationary target. Then, the person attempts to hit the same target, from the same location, while moving.
Consider a boy standing on a stationary boat (figure a., below). The boy throws a ball at a stationary target that is on shore, directly opposite the boat and parallel to it. The target has length L. To hit the target, the boy throws the ball in a line perpendicular to the axis of the boat. The ball hits the target in the center.
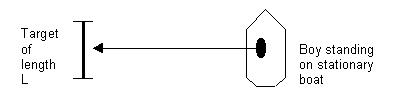
Figure a.
Now, suppose the boat is not standing still; it is moving past the target. If the boy throws the ball in exactly the same way, from the same point as before, the ball does not follow the same path as it did when the boat standing still. The speed of the moving boat will affect the ball as well, and will cause it to move farther forward, missing the target.
Assume the boy still wants to hit the target by throwing the ball in a line perpendicular to the boat, just as he did when he was standing still. He can do so, but to accomplish this, he must throw the ball before he comes alongside the target. In other words, he must adjust the time of his throw to compensate for the motion of the boat. In figure b, below, throwing the ball before the boat is alongside the target results in the ball striking the target.
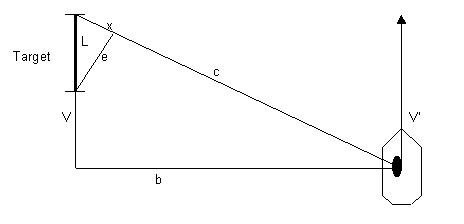
figure b.
The lines in the figure represent velocity vectors, as follows:
Even though the target has in no way changed, its "effective length" is shorter. It has been reduced by a factor of e/L , because the ball thrown by the boy in the moving boat approaches the target at an angle.
There is a theorem in geometry that says that if a line is drawn perpendicular to the side of a right triangle, the new, smaller triangle formed inside the larger one will be similar to (or, a miniature of) the larger one. We know that the effective target length was reduced by a factor of e/L. Because the two triangles are similar, we may also say that it was reduced by a factor of b/c.
The shortening effect caused by movement is not normally important when light is concerned. However, when objects move with speeds nearing the speed of light, it does become important, and leads to the special relativistic contraction. This phenomenon is analogous to the ball thrown at the target phenomenon. Using figure c, below, consider an object of length L that has a light at the front and a light at the back. If the object and the observer are stationary, an observer situated perpendicular to the object will see the distance between the lights as L. However, if the object is moving rapidly past the stationary observer, then the light from the object will approach him from an angle.
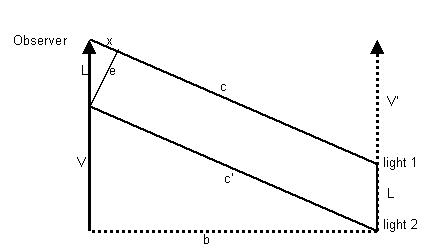
figure c.
The lines in the figure are defined, as follows:
Note: In the case of light, b is no linger a velocity vector as it was in for the thrown ball. However, for the contraction effect, that does not matter. For the effect, it is the angle on which the light approaches that is significant
The observer in this case sees the light from the two light sources arriving at an angle, so the object appears shortened by a factor of e/L. Because triangle L-e-x is similar to c-b-V, the distance between the lights (length of the object, can also be said to be shortened by a factor of b/c. So, the effective (or observed) length equal the observed length times b/c, or
Squaring both sides of the equation,
By the Pythagorean theorem,
Simplifying, we have
Taking the square root,
So, the object appears shorter by that factor. The equation derived by a physical model turns out to be identical to those determined mathematically by Lorentz, and later by Einstein.
Special Relativistic Mass Increase Derived From a Physical Model
Suppose that, as illustrated by figure d, a stationary object at point M, with mass m, is converted to light energy. The light moves to the right, and the frequency is found by a detector at point Y, which is at distance b from point M. The frequency detected at point Y is
ν
![]()
figure d.
Now suppose that, as illustrated by figure e, an identical object is moving along line V with a velocity of v with respect to a detector. The object is again converted to light at point M, and again the light moves to the right. This time, however, because of the initial motion of the object, light moves along line C, rather line B, and arrives at a detector at point X rather than at point Y.
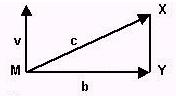
figure e.
In this case, the ratio of the lengths of line v to line c is the ratio of the object’s original velocity to the velocity of light.
The length of line c is essentially a vector representing the speed of light, while the length of line v is a vector representing the original velocity of the object with respect to the detectors at points X and Y.
Because the object was effectively moving toward the detector at point X when it became light, the detector at point X will detect a higher frequency than was found by the detector at point Y. The frequency at point X is higher because of the Doppler (blue) shift. That is, the light detected at point X came from an object that was moving toward point X.
Thus, because of the Doppler blue shift, the frequency of light detected at point X will be higher than the frequency of light from the stationary object detected at point Y by a factor of the ratio of the lengths of lines c and b:
Now, since mass can be converted to energy, and vice versa, if light coming from the object that is stationary with respect to the detector at point Y were converted back into matter, it would again have a mass of M. However, if light energy from the moving object, detected at point X, were converted back into matter, the mass produced would be greater by a factor of
where h represents Planck’s constant, and
represents frequency.
The ratio of the mass reproduced from the stationary object to the mass reproduced from the moving object then is:
squaring both sides of the equation, we have:
Now by the Pythagorean Theorem,
Taking the square root of both sides of the last equation, we have:
or
This equation, predicted using a physical model, is the same as that predicted by the mathematical approach.
If the "intuitive" idea that the observed mass of the object could not change were correct, then when the moving object was converted to light, the light would have less energy than the moving object had, and that would be a violation of the conservation of energy.
It is significant that using this physical model, in which the energy of the moving object is made equal to the energy that would result if it were converted to light (by taking the Doppler effect into account) results in the correct equation for relativistic mass increase.
Content of this paper may be freely used so long as credit is given to the author, Brian Stedjee
First publication date: September, 2003